COEFICIENTE DE PEARSON

COEFICIENTE DE CORRELACIÓN 

En estadística, el coeficiente de correlación de Pearson es una medida de la relación lineal entre dos variables aleatorias cuantitativas. A diferencia de la covarianza, la correlación de Pearson es independiente de la escala de medida de las variables.

De manera menos formal, podemos definir el coeficiente de correlación de Pearson como un índice que puede utilizarse para medir el grado de relación de dos variables siempre y cuando ambas sean cuantitativas.

EN ESTA IMAGEN SE DISTINGUEN LAS DISTINTAS REPRESENTACIONES DE LOS VALORES POSIBLES DE R

En el caso de que se esté estudiando dos variables aleatorias X y Y sobre una población; el coeficiente de correlación de Pearson se simboliza con la letra , siendo la expresión que nos permite calcularlo:

Donde:

•  es la covarianza de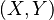 
•  es la desviación típica de la variable 
•  es la desviación típica de la variable 

De manera análoga podemos calcular este coeficiente sobre un estadístico muestral, denotado como  a: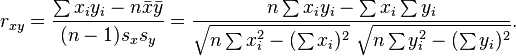

Interpretación

El valor del índice de correlación varía en el intervalo [-1,1]:

• Si r = 1, existe una correlación positiva perfecta. El índice indica una dependencia total entre las dos variables denominada relación directa: cuando una de ellas aumenta, la otra también lo hace en proporción constante.
• Si 0 < r < 1, existe una correlación positiva.
• Si r = 0, no existe relación lineal. Pero esto no necesariamente implica que las variables son independientes: pueden existir todavía relaciones no lineales entre las dos variables.
• Si -1 < r < 0, existe una correlación negativa.
• Si r = -1, existe una correlación negativa perfecta. El índice indica una dependencia total entre las dos variables llamada relación inversa: cuando una de ellas aumenta, la otra disminuye en proporción constante.